Электротехника и электроника

Введение

Процессы, протекающие в электротехнических устройствах, в общем случае подчиняются общим законам электромагнитного поля. Электромагнитные процессы, протекающие в электротехнических устройствах, сопровождаются взаимным преобразованием электромагнитной энергии в другие виды, и аналитически описываются уравнениями в частных производных (уравнениями Максвелла). Их общее решение затруднительно даже в простейших случаях. В теории электромагнитного поля оперируют с векторными величинами, такими, как плотности токов, напряженности электрического и магнитного полей.

Для исследования широкого круга устройств можно применять упрощенные методы. Их используют в электротехнике и теории электрических цепей. Они основаны на замене реального устройства некоторой упрощенной моделью, процессы в которой описываются скалярными величинами – токами, напряжениями. Отдельные элементы устройства также, заменяются моделями приближенно отражающими свойства реального элемента. Таким образом, электротехника занимается упрощенными методами исследования и расчета электромагнитных явлений и устройств на их основе, процессы в которых описываются  электрическими токами и напряжениями.

Электротехника имеет два направления. Они имеют общую физическую основу, но направлены на решение различных технических задач. Силовая электротехника – это производство и передача электрической энергии и преобразование ее в другие виды: механическую, тепловую, световую. Информационная электротехника - направлена на использование электрических явлений для передачи и обработки информации. Второе направление называют радиоэлектроникой, информационной электроникой, оно изучается в курсе теория электрических цепей и рассмотрено в настоящем пособие.

ГЛАВА 1

Основные понятия, определения и законы

в теории электрических цепей

1.1 Схема обобщенной электрической цепи

Любое электронное устройство состоит из простых, заранее изготовленных элементов. Совокупность таких элементов, соединенных определенным образом и предназначенных для протекания по ним электрического тока называется электрической цепью.

Все элементы электрической цепи можно разбить на две группы:

1)  Источники электрической энергии или электрических сигналов - создают электрический сигнал. Их называют активными элементами.

2) Приёмники электрической энергии (нагрузка) – поглощают электрическую энергию, совершая полезную работу. Их называют пассивными элементами.

Обобщённая электрическая цепь представлена на рис. 1.1. в виде схемы. В ее состав входят:

1)                


Источники электрической энергии или электрических сигналов – служит для создания электрических сигналов.

2) Приёмники электрической энергии (нагрузка) – это какое-либо исполнительное устройство.

3)       Линия связи - служит средством передачи сигнала источника сигнала в нагрузку. Она состоит, как из активных и пассивных элементов.

Каждый из элементов этой схемы можно рассматривать как электрическую цепь. Чаще всего под электрической цепью в информационной технике понимают линию связи. Сигнал x(t) на входе линии связи называют входным сигналом или воздействием, а сигнал y(t) на выходе называют выходным, откликом или реакцией цепи.

Схема (модель) электрической цепи –  представляет собой условное графическое изображение электрической цепи. Различают различные типы схем:

Структурная схема – это условное графическое изображение реальной цепи в виде прямоугольников или условно- графических обозначений (УГО), отражающих только важнейшие функциональные части цепи и основные связи между ними.

Принципиальная схема – показывает в виде УГО все элементы цепи и порядок соединения между ними.

Схема замещения или эквивалентная схема - составляется из УГО идеализированных элементов, которые заменяют исследуемую реальную цепь в рамках решаемой задачи.  

1.2. Основные понятия электрической цепи

Электрические процессы, протекающие в электрической цепи, характеризуются следующими понятиями.

Электрический ток - есть упорядоченное, направленное движение свободных носителей зарядов.


Ток характеризуется величиной и направлением. За положительное направление тока принято движение положительных зарядов. Ток неизменный во времени обозначается - I, а переменный - i(t). Единица измерения - Ампер [A]. Также применяют  следующие единицы измерения:

мА = 10-3 А, где  м – милли; мкА = 10-6 А, мк – микро;

нА = 10-9 А, н – нано; рА = 10-12 А,  р – пико.

Электрический заряд. При протекании электрического тока через поперечное сечение проводника S за время t переносится определенное количество электричества, то есть электрического заряда. Заряд обозначается - q, или Q = It,. Единица измерения заряда – Кулон [Кл]. Т.о. электрический ток, есть заряд прошедший через заданное сечение проводника за единицу времени:

I=Q/t, .

Электрический потенциал – энергия, которая затрачивается на перемещение единичного положительного электрического заряда из бесконечности в заданную точку электрической цепи. Обозначается ?, единица измерения - Вольт [В].

Напряжение на участке цепи - есть разность потенциалов, на выводах этого участка:          U12 = ?1 - ?2. Напряжение рассматривается как физическая причина, обуславливающая возникновение тока в цепи. При протекании по участку цепи (рис. 1.2.) электрического тока, на нем возникает падение напряжения. За положительное направление напряжения принято направление в сторону уменьшения потенциала (?1> ?2), т.е. оно совпадает с направлением тока. Напряжение указывают стрелкой или знаками + и -. Если ?1 < ?2, то напряжение имеет отрицательный знак U21 = -U12 . Напряжению можно дать и другое определение. Напряжение – это энергия, которое необходимо затратить на перемещение единичного положительного заряда из одной точки цепи в другую, т.е. оно определяется как отношение энергии W (dW), необходимой для перемещения положительного заряда q (dq) из одной точки цепи в другую, к величине этого заряда т. е.

U =  , или  u = .

ЭДС (электродвижущая сила)– это напряжение, которое создается между двумя точками электрической цепи за счет действия некоторых сторонних сил.


Эти силы обычно имеют неэлектрическую природу. За положительное направление ЭДС принимают направление в сторону возрастания потенциалов. Элементы создающие ЭДС называют источниками ЭДС. Условное обозначение показано на рис. 1.3. Стрелка в окружности показывает направление возрастание потенциала; напряжение на источнике ЭДС направлено встречно направлению ЭДС , но учитывая его положительное направление имеем

U = E .

Это позволят задавать величину ЭДС через напряжение.

Энергия, выделяемая или поглощаемая, на участке электрической цепи  обычно выражают через основные электрические характеристики –напряжение и ток. Учитывая, что dw=u dq и dq=i dt после интегрирования имеем

w(t) = .

Единица измерения энергии джоуль -  [Дж].

 Мощность – есть скорость изменения энергии. Единица измерения мощности - Ватт [Bт].

                                            р(t) = = ui.

Если р(t) = ui > 0, то на данном участке происходит поглощение мощности, его энергии увеличивается. Данный участок является потребителем энергии и называется пассивным.

Если ui < 0, то происходит выделение мощности, энергии  на данном участке уменьшается. Данный участок содержит источники энергии и называется активным.

Информация – это сведения о поведении интересующего нас события, объекта или явления. Информация не материальна.

Сигнал – это физический процесс, который предназначен для передачи информации на расстояние. Это физический процесс способный распространяться в пространстве.

1.3. Основные законы электрических цепей

Электрические процессы, протекающие в электрических цепях, подчиняются следующим законам.

Закон Ома. Он устанавливает связь между напряжением u= ?1-?2 и током i на участке цепи (рис. 1.4.) i=F(u), например, для цепи постоянного тока (i=I), он записывается так:

  

где  G - проводимость участка цепи, единица измерения проводимости - Сименс [См]. R =1/G- сопротивление участка цепи, единица измерения - Ом [Ом].

Так как простейший участок цепи состоит из одного элемента, то закон Ома является уравнением элемента.



Первый закон Кирхгофа. Устанавливает связь между токами ветвей в узле электрической цепи. Узел – это точка соединения двух или более элементов. Ветвь - это участок цепи, который включен между двумя узлами, по которому протекает общий для всех элементов ток.

Для узла выполняется закон сохранения заряда – сколько заряда переносится к узлу втекающими токами, столько же заряда выходит из узла, т.е. в узле заряды не накапливаются и не исчезают.

 Первый закон Кирхгофа звучит так: алгебраическая сумма токов ветвей в узле электрической цепи, в любой момент времени, равна нулю.

,

где n – номер ветви в узле.

Слагаемые суммы берут: со знаком «+» - если токи втекают в узел, и со знаком « - » - если токи вытекают.

 Для схемы на рис.1.5 первый закон Кирхгофа записывается  так:

I1+I2+I3- I4=0.

 Второй закон Кирхгофа. Устанавливает связь между напряжениями на элементах контура (рис. 1.6). Контур состоит из ветвей, образующих замкнутый путь для протекания электрического тока. Второй закон Кирхгофа: алгебраическая сумма напряжений на элементах контура, в любой момент времени равна нулю.

,

где k – номер элемента контура.

Второй закон Кирхгофа является следствием закона сохранения энергии, т. е. энергия создаваемая источниками и теряемая на пассивных элементах контура одинакова.

Для записи 2-го закона Кирхгофа необходимо:

1. Выбрать условно - положительное направление обходов элементов контура (обычно, почасовой стрелке).

2. Указать положительное направление напряжения на элементах контура.

3. Записать алгебраическую сумму напряжений, в которой со знаком  «+» берут те напряжения, которые совпадают с направлением обхода контура, и со знаком «-», те напряжения которые не совпадают.

Для схемы на рис. 1.6 второй закон Кирхгофа записывается так:

                                   UR1 + UR2 – E1+Е2 = 0

Часто используют другую формулировку второго закона Кирхгофа. Алгебраическая сумма падений напряжений (u) на элементах контура равна алгебраической сумме источников ЭДС, входящих в контур.





где n – номер пассивного элемента контура, k - номер активного элемента контура. Для схемы на рис. 1.6 второй закон Кирхгофа по второй форме записи записывается так:

.

Для записи 2-го закона Кирхгофа необходимо:

1. Выбрать условно - положительное направление обходов элементов контура (обычно, почасовой стрелке).

2. Записать алгебраическую сумму падений напряжений, в которой со знаком  «+»  берутся те падения напряжения, которые совпадают с направлением обхода контура, и со знаком « - », те падения напряжений которые не совпадают.

3. Записать алгебраическую сумму источников эдс, в которой со знаком  «+»  берутся те эдс, которые совпадают с направлением обхода контура, и со знаком « - », те эдс  которые не совпадают.

Так как законы Кирхгофа устанавливают взаимосвязи токов и напряжении при различных способах соединения элементов, то уравнения составленные по законам Кирхгофа называют уравнениями соединений.

ГЛАВА 2

Математические модели сигналов

Сигнал характеризует поведение интересующего нас объекта, а потому он может быть описан некоторой функцией:

1.          -  временная функция.

2.         -  пространственно-временная функция.

В дальнейшем будем рассматривать лишь временные сигналы.

2.1. Классификация электрических сигналов

1.        По характеру их изменения во времени и по величине.

Сигналы разделяются на непрерывные (аналоговые) и импульсные.

Аналоговый сигнал описывается функцией произвольной по величине и непрерывной во времени.

Импульсные сигналы – это сигналы, существующие не на всей временной оси, или это сигналы описываются функциями с разрывами.

Импульсные сигналы подразделяются на следующие:

1)     дискретные;

2) квантованные;

3)  цифровые.

На рис.2.1. показаны временные диаграммы аналогового, дискретного, квантованного и цифрового сигналов.

На рис.2.1а приведен фрагмент аналогового сигнала.

  Дискретный  - сигнал (рис.2.1б).


Это сигнал, произвольный по величине и дискретный во времени.

При дискретизации непрерывный сигнал заменяется своими отсчетами – S(n?t), взятыми с шагом ?t – шаг дискретизации.

Для того чтобы непрерывный сигнал дискретизировать, а затем по этим отсчетам восстановить исходный аналоговый сигнал, – шаг дискретизации ?t  должен удовлетворять следующему условию:

, Fmax - максимальная частота в исходном аналоговом сигнале. (Это соотношение называется теоремой Котельникова).

3)  Квантованный – сигнал (рис.2.1в). Это сигнал непрерывный во времени, но дискретный по величине. Для его получения ось значений сигнала разбивают на фиксированные уровни (уровни квантования). При квантовании мгновенным значениям аналогового сигнала ставят в соответствие ближайший разрешенный уровень. ?x - шаг квантования (?x=xn+1-xn). Величину шага квантования выбирают исходя из величины помехи, которая, накладываясь на исходный сигнал, искажает его форму. Чтобы искажений за счет помех не было, шаг квантования выбирают из соотношения: .

4)                 Цифровые – сигналы (рис.2.1г). Это сигналы, квантованные по величине и дискретные во времени.  Передача такого сигнала заменяется передачей цифр, соответствующих уровням квантования в дискретные моменты времени.

2.      Классификация по способу математического описания.

Классификация показана на рис.2.2.



Детерминированные сигналы задаются некоторой аналитической функцией времени S(t). С точки зрения передачи информации такой сигнал никакой информации не несет, поскольку для любого момента времени t1 можно заранее подсчитать значение сигнала S(t1). Такие сигналы применяются:

-как управляющие сигналы, в различных системах управления;

-как испытательные, в устройствах выделения информации, для определения их характеристик. Проходя через цепь, сигнал искажается. По искажениям сигнала можно оценивать свойства устройства, то есть испытывать (определять)  характеристики устройства.



 Примеры периодических сигналов.

1) Периодическая последовательность прямоугольных импульсов (рис.2.3). Ее параметры:  Am – амплитуда;  - длительность импульса; T  - период. Это пример импульсного сигнала.

2)Гармонические колебания (рис.2.4.).

S(t) = Amcos(wt - j0)

 Его параметрами являются Am – амплитуда , w - частота, j0 – начальная фаза. Это пример  непрерывного сигнала.

Непериодические сигналы – это сигналы, которые описываются непериодическими функциями времени. Однако их можно рассматривать как периодические, для которых Т .

Примеры непериодических сигналов.

1)  Сигнал типа единичная функция (ступенчатый сигнал, функция Хевисайда, рис.2.5.).

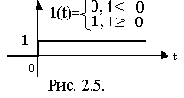
2) Одиночный прямоугольный импульс –это сигнал, форма которого прямоугольная (рис.2.6).

 3) Сигнал типа  (дельта – функция, функция Дирака, рис. 2.7.).

                   0, t<0

   (t)=     , t=0         

                  0, t>0

Он обладает свойствами:  1.;

2.-это соотношение называют, фильтрующее свойство дельта – функции.

Случайные сигналы – это сигналы характер изменения, которых заранее предсказать невозможно. Именно эти сигналы несут новую информацию о состоянии интересующего нас объекта. С математической точки зрения эти сигналы описываются методами теории вероятности или случайных процессов. Разновидностью случайных сигналов являются помехи – сигналы, которые накладываются на передаваемые сообщения и искажают его характер. Помехи бывают: атмосферными, индустриальными и флуктуационными.

 Флуктуационные помехи связаны с процессами, происходящими в элементах электрических цепей, а именно, с движением свободных носителей зарядов в них.

2.2. Гармоническое колебание и способы его представления

Гармонический сигнал – это сигнал, который описывается гармонической функцией времени: sin(t), cos(t).

Гармоническое колебание, а также сигнал произвольной формы могут быть представлены в следующих формах:

1) временное представление сигнала;

2) комплексное представление;

3) векторное представление;



4) спектральное;

5) операторное.

1) При временном представлении сигнал записывается в виде аналитической функцией времени: .

Его график – зависимость от времени – называется временной диаграммой (рис.2.8.). Основными параметрами гармонического сигнала являются:

1.      Амплитуда - Am (наибольшее отклонение от нуля гармонической функции). Размерность амплитуды связана с физической природой сигнала.

2. Период - T (минимальное расстояние между точками находящимися в одной фазе), ?=2?/T - круговая частота, f=1/T – циклическая частота. Их размерность: T ® [сек];  f ® [Гц]; ? ® [рад/сек].

3.   j0=?t0 – начальная фаза гармонического колебания гармонического колебания; t0 – временной сдвиг, если t0>0, то это означает опережение, если t0<0, то это означает задержку сигнала.

4.    (?t + ?0) – полная фаза гармонического колебания.

2) При комплексном представлении гармоническое колебание, как функция времени, заменяется комплексной амплитудой, т. е. комплексным числом независящим от времени. Это делается для упрощения записи и операций над гармонической функции.

Вспомним комплексные числа.   - комплексное число. Его можно записать в одной из трех форм: алгебраической, показательной и тригонометрической.

  =

 где      

    - реальная часть, - мнимая часть комплексного числа. На рис. 2.9 показано геометрическое представление комплексного числа на комплексной плоскости.

 А – mod[Z] – модуль комплексного числа Z, или А=(а2+b2)1/2  - длины  вектор комплексного числа.

? =arg[Z] – аргумент комплексного числа Z, или  ? = arctg(b/a) – начальная фаза.

Выражение Аmej(?t+?)  называют комплексом гармонической функции. Тогда учитывая, что Аcos? = Re{Aej?}, можно записать



Комплексную величину называют комплексной амплитудой гармонического сигнала, а еj?t – множитель вращения. Комплексная амплитуда содержит информацию о двух важнейших параметрах гармонического сигнала – об амплитуде и о начальной фазе. Комплексная амплитуда и гармоническая функция времени, при известной частоте связаны однозначно, т.


е.

.

Например: гармоническому колебанию u(t)=256cos(2?100t - 450) соответствует комплексная амплитуда- Ùm = 256e-j45.

3) Векторное представление – это представление сигнала вектором на комплексной плоскости. При расчетах удобно использовать следующие понятия о гармоническом сигнале:

а) комплексное гармоническое колебание - гармонический комплекс:

s(t)= Аmej(?t+?)= Åmej(?t)    ,

где ej?t – множитель вращения. На комплексной плоскости гармонический комплекс представляется вектором  Аm c  начальной фазой ?0 вращающимся против часовой стрелки с частотой ?.

б) гармоническое колебание s(t) = Amcos(?t+?0) = Re{Åmej?}. На комплексной плоскости гармоническое колебание представляется проекцией    вращающегося с частотой ? против часовой стрелки вектора гармонического комплекса  на реальную ось.

в) Комплексная амплитуда . На комплексной плоскости она  представляется в виде неподвижного вектора с амплитудой Am и начальной фазой j0.

5)       Спектральное представление сигнала.

6)     Операторное представление сигнала.

Два последних способа описания сигнала рассмотрим подробнее.

2.3. Спектральное представление сигналов

Спектральный способ представления сигнала S(t) основан на представление любой функции времени совокупностью гармонических составляющих с соответствующими амплитудами, частотами и начальными фазами. При спектральном представление сигнал задаётся не как функция времени, а как функция частоты, что является очень удобным, поскольку свойства электрических цепей часто задаются их частотными характеристиками.

Спектры периодических сигналов

Сигналы, удовлетворяющие условию S(t)=S(t+T), если  Т < ?, а -?<t<+?  называются периодическими. Простейшим периодическим сигналом являются гармонические колебания S(t)=Amcos(?0t+j0). Оно состоит из одной гармонической составляющей с амплитудой Am и начальной фазой j0, которые расположены на частоте ?0. Для наглядного изображения спектров сигналов их изображают в виде графиков, при этом рассматривают по отдельности амплитудный спектр и фазовый спектр.



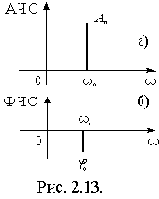
Амплитудный или амплитудно-частотный спектр (АЧС) - это зависимость амплитуд гармонических составляющих от частоты (АЧС>Amn(?), рис 2.13а).

Фазово-частотный спектр (ФЧС) – это зависимость начальных фаз гармонических составляющих от частоты (ФЧС>j(?), рис. 2 13б).

Из математики известно, что любой периодический сигнал S(t) удовлетворяющий условиям Дирихле может быть представлен тригонометрическим рядом Фурье



где  (T – период сигнала) – основная частота сигнала (первая гармоника сигнала), n – номер гармоники сигнала, n? – частота n-ой гармоники сигнала, - коэффициенты ряда Фурье:

 - постоянная  (средняя) составляющая сигнала;

 - амплитуда n-ой косинус составляющей спектра сигнала;

 - амплитуда n-ой синус составляющей спектра сигнала;

 - амплитуда n-й гармоники;

 - начальная фаза n-ой гармоники.

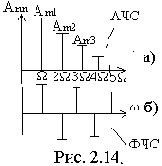
Из ряда Фурье следует, что спектр периодического сигнала имеет дискретный (линейчатый) характер по оси частот (рис. 2.14).

Спектры непериодических сигналов

Сигнал, у которого S(t)= S(t+T) при T>? называется  непериодическим. Непериодический сигнал в ряд Фурье разложить нельзя, для него вводится интеграл Фурье, который является пределом ряда при T>?.

При переходе к пределу ряда, когда T>?:

1.)= >0 это означает что расстояние между спектральными линиями стремится к нулю, т.е. спектр становиться сплошным.

2.), т. е. спектр оказывается состоящий из гармонических составляющих с бесконечно малой амплитудой.

В целом спектр непериодического сигнала характеризуется функцией спектральной плотности. Она показывает плотность распределения бесконечно малых амплитуд по оси частот, т.е. показывает сколько гармонических составляющих с бесконечно малыми амплитудами приходится в диапазон частот df.

 Функция спектральной плотности S(j?) связана с сигналом S(t) преобразованием Фурье:

 - прямое преобразование Фурье (ППФ).

 - обратное преобразование Фурье (ОПФ).

Функция спектральной плотности это комплексная функция частоты

S(j?)= S(?)ej?(?),



где S(?) – модуль функции спектральной плотности, его называют спектральной плотностью амплитуд; ?(?) – аргумент функции спектральной плотности – спектр фаз.

Главной особенностью спектра непериодического сигнала является его сплошной, непрерывный характер.

 Пример. Найти S(j?) одиночного прямоугольного импульса (рис. 2.15).

По временной диаграмме запишем аналитическое выражение такого сигнала:



Найдем функцию спектральной плотности импульса и приведем это выражение к функции типа .



 Спектральная плотность амплитуд импульса (рис. 2.16) имеет вид 

.

Большинство сигналов имеет бесконечный спектр по оси частот. В то же время для них применяют понятие о ширине спектра, т.е. считают, что спектры у таких сигналов ограничены. Под шириной спектра понимают диапазон частот в котором сосредоточена заданная доля  от энергии всего сигнала (50, 90, 95, 99)% .

Для одиночного прямоугольного импульса за ширину спектра принимают интервал частот от 0 до 2p/?u     т.е. граничная частота верхняя wгр= 2p/?u .   

Таким образом ?u и wгр связана соотношением – чем короче импульс тем шире его спектр сигнала.

2.4. Операторное представление сигнала

          Преобразование Фурье применяется лишь для сигналов с конечной энергией, т. е. для сигналов удовлетворяющих условию

.

Функция S(t), удовлетворяющая записанному условию называется абсолютно интегрируемой.

Более универсальным является операторное представление сигнала, которое основано на преобразование Лапласа. При операторном представление, сигналу S(t), как функции действительной переменной t, ставится в соответствие функция комплексной переменной р - S(p), где, p= ?+j? (p - называется комплексная частота). Эта функция вводится следующим выражением:

 - прямое преобразование Лапласа (ППЛ), (S(p)=L[S(t)]), 

 - обратное преобразование Лапласа (ОПЛ), (S(t)=L-1[S(p)]).

S(t) –называют оригиналом или сигналом, а S(p) – изображением или операторным представлением сигнала.

Для нахождения функции спектральной плотности S(j?) по известному операторному представлению S(p)  сигнала необходимо р заменить на j?, т.е.


S(j?) = S(р)|р= j? .

Пример. Найти спектральную плотность S(j ?) для единичной функции.

                   

 

2.5. Свойства преобразований Фурье и Лапласа.

Так как преобразования Фурье и Лапласа схожи, рассмотрим свойства только преобразования Фурье.

1). Спектр суммы сигналов  равен сумме спектров этих сигналов, т.е.

S1(t)>S1(j ?); S2(t)>S2(j ?); S(t)=S1(t)+S2(t)>S(j ?)=S1(j?)+S2(j ?)

Это вытекает из  свойства линейности преобразования Фурье ПФ.

2). Спектр сигнала сдвинутый по оси  времени на время tз (время задержки), равен спектру исходного сигнала, домноженного на множитель  .


т.е. если S1(t)>S(j ?), то S2(t)=S1(t-tз)>S1(j ?) .   

На рис.2.18 приведены сигналы: без сдвиг (рис.2.18 а), сигнал с задержкой на время t0  (рис.2.18 б) и сигнал с опережением на время t0  (рис. 2.18 в)

3).Изменение масштаба сигнала по оси времени приводит к изменению масштаба его спектра по оси частот

 S1(t)>S1(j ?);  S2(t)=S1(?t)>S2(t)=   S1(j ? /?)

? >1 - сжатие сигнала по оси времени, приводит к растяжению его спектра по оси частот

0< ?<1 - растяжение сигнала по оси времени, приводит к сжатию его спектра по оси частот

Пример:  S1(t)=cos ?t; S2(t)=cos2 ?t.

4). Дифференцирование сигнала эквивалентно умножению его спектра на множитель j?.

Пусть сигнал S1(t) имеет спектральную плотность S1(j?), (S1(t) > S1(j?)), тогда S2(t)=d(S1(t))dt > S2(jw) =  jw S1(j?).

При дифференцировании выделяются высокочастотные составляющие спектра сигнала, а низкочастотные ослабляются, т.к. имеют малый масштабный множитель.

5). Интегрирование сигнала эквивалентно умножению спектра на множитель 1/j?.

Пусть сигнал S1(t) имеет спектр S1(jw), (S1(t) > S1(j?)), тогда

S2(t)=S1(t)dt > S2(jw) =  (1/jw)S1(j?)).

При интегрировании выдаются низкочастотные составляющие, а высокочастотные – подавляются.

2.6. Модулированные сигналы и их спектры. Радиосигналы

Для передачи информации на большие расстояния требуются электро­магнитные колебания, которые эффективно излучаются антенными устрой­ствами и способны распространяться в свободном пространстве с малым затуханием.


Такими сигналами являются высокочастотные колебания. Среди них наиболее распространенными в радиотехнике являются гармонические колебания.

Чисто гармоническое колебание представляет собой детерминиро­ванную функцию и не содержит никакой информации. Такое колебание называется несущим.

Чтобы превратить высокочастотное гармоническое колебание в радиосигнал, нужно заложить информацию в несущее колебание, т.е. промодулировать его по закону передаваемого сообщения.

Кроме того, необходимо рационально выбрать частоту несущего колебания . Обычно   (?max - максимальной частоты видеосигнала). Чем уже полоса частот сигнала по сравнению с несущей частотой, тем меньше искажений вносится в радиосигналы при передаче их через  радиотехнические устройства.

Поэтому в связи с непрерывно возрастающей сложностью передаваемой информации и с увеличением максимальной частоты спектра видеосигнала для современной радиотехники характерно повышение несущих частот.

В общем случае радиосигнал можно представить в виде  , где амплитуда A или полная фаза =?t+? изменяются по закону передаваемого сообщения. Процесс управления  параметрами несущего колеба­ния по закону передаваемой информации называется модуляцией, а колебание - модулированным. Различают амплитудную и угловую модуляцию. Угловая модуляция подразделяется на частотную и фазовую.

Амплитудная модуляция.

, где  - постоянная амплитуда высокочастотного колебания, коэффициент пропорциональности.

,

где  - постоянная угловая частота,  - постоянная начальная фаза

В общем случае S(t) носит случайный характер, но для выявления основных характеристик AM колебаний, будем полагать, что и огибающая является детерминированной функцией.

Пусть управляющий видеосигнал - чисто гармоническое низкочастот­ное колебание

Такое колебание называется тонально модулированным.

Пусть  тогда



Здесь ,

 M - коэффициент модуляции или глубина модуляции

Для неискаженной передачи:  

Спектр амплитудно-модулированного колебания легко определить



На рис преедставлен спектр





Частотная и фазовая модуляция (ЧМ и ФМ)

При этих видах модуляции по закону передаваемого сообщения изменяется аргумент, т.е. полная фаза . 

При ЧМ    

Для случая тональной модуляции



-девиация частоты (максимальное отклонение частоты от исход­ного значения)

, где   - индекс частотной модуляции

При ФМ   

 Для тональной ФМ при

 - индекс базовой модуляции,

Оба вида модуляции (при тональной модуляции) могут быть выражены одинаково

Временные диаграммы ЧМ и ФМ сигналов не различаются.

Рассмотрим спектр высокочастотного колебания при тональной угловой модуляции:



При m<<1