Логические схемы и функции
Цель работы
1. Исследование логических схем.
2. Реализация логических функций при помощи логических элементов.
3. Синтез логических схем, выполняющих заданные логические функции.

Краткие сведения из теории
1. Аксиомы алгебры логики. Переменные, рассматриваемые в алгебре логики, могут принимать только два значения - 0 или 1. В алгебре логики определены: отношение эквивалентности (обозначается знаком =) и операции: сложения (дизъюнкции), обозначаемая знаком v, умножения (конъюнкции), обозначаемая знаком & или точкой, и отрицания (или инверсии), обозначаемая надчеркиванием или апострофом'. Алгебра логики определяется следующей системой аксиом:

2. Логические выражения. Запись логических выражений обычно осуществляют в конъюнктивной или дизъюнктивной нормальных формах. В дизъюнктивной форме логические выражения записываются как логическая сумма логических произведений, в конъюнктивной форме - как логическое произведение логических сумм. Порядок действии такой же, как и в обычных алгебраических выражениях. Логические выражения связывают значение логической функции со значениями логических переменных. 3. Логические тождества. При преобразованиях логических выражений используются логические тождества:

4. Логические функции. Любое логическое выражение, составленное из п переменных xn,xn-1... X1 с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию п переменных. Такую функцию называют логической. В соответствии с аксиомами алгебры логики функция может принимать в зависимости от значения переменных значение 0 или 1. Функция п логических переменных может быть определена для 2" значений переменных, соответствующих всем возможным значениям п-разряд-ных двоичных чисел. Основной интерес представляют следующие функции двух переменных х и у:





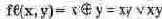
5. Логические схемы. Физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию, называется логическим элементом. Схема, составленная из конечного числа логических элементов по определенным правилам, называется логической схемой. Основным логическим функциям соответствуют выполняющие их схемные элементы.
6. Таблица истинности. Так как область определения любой функции п переменных конечна (2n значений), такая функция может быть задана таблицей значений f(Vi), которые она принимает в точках Vi, где i= 0,1. -.2n—1. Такие таблицы называют таблицами истинности. В таблице 12.1 представлены таблицы истинности, задающие указанные выше функции.
Таблица 12.1
i
i= 2х+у - число, образованное значениями переменных.
7. Карты Карно и диаграммы Вейча. Если число логических переменных не превышает 5-6, преобразования логических уравнений удобно производить с помощью карт Карно или диаграмм Вейча. Цель преобразований - получение компактного логического выражения (минимизация). Минимизацию производят объединением наборов (термов) на карте Карно. Объединяемые наборы должны иметь одинаковые значения функции (все 0 или все 1). Для наглядности рассмотрим пример: пусть требуется найти логическое выражение для мажоритарной функции fm трех переменных X, Y, Z, описываемой следующей таблицей истинности:
Таблица 12.2. Мажоритарная функция
N
Составим карту Карно. Она представляет собой нечто похожее на таблицу, в которой наименования столбцов и строк представляют собой значения переменных, причем переменные располагаются в таком порядке, чтобы при переходе к соседнему столбцу или строке изменялось значение только одной переменной. Например, в строке XY таблицы 12.3 значения переменных XY могут быть представлены следующими последовательностями: 00,01,11,10 и 00,10,11,01. Таблицу заполняют значениями функции, соответствующими комбинациям значений переменных. Полученная таким образом таблица выглядит, как показано ниже (таблица 12.3). Таблица 12.3. Карта Карно мажоритарной функции

На карте Карно отмечаем группы, состоящие из 2n ячеек (2, 4, 8,...) и содержащие 1, т. к. они описываются простыми логическими выражениями. Три прямоугольника в таблице определяют логические выражения XY, XZ, YZ. Каждый прямоугольник, объединяющий две ячейки, соответствует логическим преобразованиям:

Компактное выражение, описывающее функцию, представляет собой дизъюнкцию полученных при помощи карт Карно логических выражений. В результате получаем выражение в дизъюнктивной форме: fm = XY v XZ vYZ. Для реализации функции мажоритарной логики трех логических переменных необходимо реализовать схему, которая при подаче на ее входы трех сигналов формировала бы на выходе сигнал, равный сигналу на большинстве входов (2 из 3 или 3 из 3). Эта схема полезна для восстановления истинного значения сигналов, поступающих на 3 входа, если возможен отказ на одном из входов. Для реализации функции на элементах 2И-НЕ преобразуем полученное выражение в базис элементов И-НЕ, т. е. запишем выражение при помощи операций логического умножения и инверсии. Проверить справедливость каждого из приведенных выражений для fm можно прямой подстановкой значений X, Y, Z из таблицы 12.2:
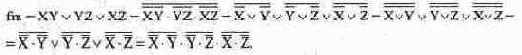
Соответствующая схемная реализация приведена на рис. 12.1.

Порядок проведения экспериментов Эксперимент 1. Исследование логической функции И. а). Задание уровней логических сигналов. Откройте файл с12_01 со схемой, изображенной на рис. 12.2. В этой схеме два двухпозиционных переключателя А и В подают на входы логической схемы И уровни 0 (контакт переключателя в нижнем положении) или 1 (контакт переключателя в верхнем положении). Включите схему. Установите переключатель В в нижнее положение. Измерьте вольтметром напряжение на входе В и определите с помощью логического пробника уровень логического сигнала. Установите переключатель В в верхнее положение. Определите уровень логического сигнала и запишите показания вольтметра; укажите, какой логический сигнал формируется на выходе Y. Результаты занесите в раздел "Результаты экспериментов".

б). Экспериментальное получение таблицы истинности элемента И. Подайте на входы схемы все возможные комбинации уровней сигналов А и В и для каждой комбинации зафиксируйте уровень выходного сигнала Y. Заполните таблицу истинности логической схемы И (табл. 12.4 в разделе "Результаты экспериментов"). в). Получение аналитического выражения для функции. По таблице 12.4 составьте аналитическое выражение функции элемента И и занесите его в раздел "Результаты экспериментов".
Эксперимент 2. Исследование логической функции И-НЕ. а). Экспериментальное получение таблицы истинности логического элемента 2И-НЕ, составленного из элементов 2И и НЕ. Соберите схему, изображенную на рис. 13.3. Включите схему. Подайте на входы схемы все возможные комбинации уровней входных сигналов и, наблюдая уровни сигналов на входах и выходе с помощью логических пробников, заполните таблицу истинности логической схемы 2И-НЕ (табл. 12.5 в разделе "Результаты экспериментов").

б). Экспериментальное получение таблицы истинности логического элемента 2И-НЕ. Соберите схему, изображенную на рис. 12.4. Включите схему. Подайте на входы схемы все возможные комбинации уровней входных сигналов и, наблюдая уровни сигналов на входах и выходе с помощью логических пробников, заполните таблицу истинности логической схемы 2И-НЕ (табл. 12.6 в разделе "Результаты экспериментов"). Сравните таблицы 12.5 и 12.6 между собой.

Эксперимент 3. Исследование логической функции ИЛИ. а). Экспериментальное получение таблицы истинности логического элемента ИЛИ. Соберите схему рис. 12.5. Включите схему. Подайте на входы схемы все возможные комбинации уровней входных сигналов и, наблюдая уровни сигналов на входах и выходе с помощью логических пробников, заполните таблицу истинности логической схемы ИЛИ (табл. 12.7 в разделе "Результаты экспериментов"). б). Получение аналитического выражения для функции. По таблице 12.7 составьте аналитическое выражение функции и занесите его в раздел "Результаты экспериментов".

Эксперимент 4. Исследование логической функции ИЛИ-НЕ. а). Экспериментальное получение таблицы истинности логического элемента 2ИЛИ-НЕ, составленного из элементов 2ИЛИ и НЕ. Соберите схему, изображенную на рис. 12.6. Включите схему. Подайте на входы схемы все возможные комбинации уровней входных сигналов и, наблюдая уровни сигналов на входах и выходе с помощью логических пробников, заполните таблицу истинности логической схемы 2ИЛИ-НЕ (табл. 12.8 в разделе "Результаты экспериментов").

б). Экспериментальное получение таблицы истинности логического элемента 2ИЛИ-НЕ. Соберите схему, изображенную на рис. 12.7. Включите схему. Подайте на входы схемы все возможные комбинации уровней входных сигналов и, наблюдая уровни сигналов на входах и выходе с помощью логических пробников, заполните таблицу истинности логической схемы 2ИЛИ-НЕ (табл. 12.9 в разделе "Результаты экспериментов"). Сравните таблицы 12.8 и 12.9 между собой.

Эксперимент 5. Исследование логических схем с помощью генератора слов. а). Сведения об исследуемой микросхеме. Откройте файл с12_02 со схемой, изображенной на рис. 12,8. Включите схему. Укажите, к каким выводам микросхемы 7400 подключается источник питания, сколько элементов 2И-НЕ содержит микросхема, сколько элементов используется в данном эксперименте и как обозначены на схеме используемые входы и выходы. Заполните таблицу сведений о микросхеме (табл. 12.10 в разделе "Результаты экспериментов").

б). Экспериментальное получение таблицы истинности логического элемента 2И-НЕ. Запрограммируйте генератор слов так, чтобы на выходе генератора получать последовательно следующие комбинации:00, 01, 10, 11. Переведите генератор в режим пошаговой работы нажатием кнопки "Step" на увеличенном изображении генератора. Каждое нажатие кнопки "Step" вызывает переход к очередному слову заданной последовательности, которое подается на выход генератора. Последовательно подавая на микросхему слова из заданной последовательности, заполните таблицу истинности элемента 2И-НЕ (табл. 12.11 в разделе "Результаты экспериментов").

Эксперимент 6. Реализация логической функции 3-х переменных. а). Синтез схемы., реализующей функцию, заданную логическим выражением. Реализуйте функцию f = ab v bc на элементах 2И-НЕ.

Соберите в Electronics Workbench схему на элементах 2И-НЕ, соответствующую полученному выражению. Подключите к входам схемы генератор слов, к выходу - логический пробник. Генератор слов запрограммируйте на формирование последовательности из восьми слов, соответствующих числам от 0 до 7: 0=000; 1=001; 2=010; 3=011; 4=100; 5=101; 6=110; 7=111. В пошаговом режиме, последовательно подавая на вход полученной схемы все слова последовательности, определите при помощи логического пробника уровень сигнала на выходе схемы. По полученным результатам заполните таблицу 12.12 в разделе "Результаты экспериментов".
6). Синтез схемы, реализующей заданную функцию при помощи логического преобразователя. Для получения схемы, реализующей функцию, описываемую логическим выражением f = ab v bc , можно воспользоваться логическим преобразователем.
Для этого проделайте следующее: • вызовите логический преобразователь • введите в нижнее окно панели преобразователя логическое выражение ab v be с клавиатуры (операции ИЛИ соответствует знак +, инверсия обозначается апострофом); • для реализации схемы на элементах И-НЕ нажмите клавишу А В —> NAND на панели логического преобразователя.
Логический преобразователь выводит на рабочее поле схему, реализующую функцию, описываемую введенным логическим выражением. Полученная схема приведена на рис. 12.9. К схеме подключите генератор слов, запрограммированный на формирование восьми слов, соответствующих числам от 0 до 7: 0=000; 1=001; 2=010; 3=011; 4=100; 5=101; 6=110; 7=111. Переведите генератор слов в пошаговый режим. Включите схему. Последовательно подавая на входы схемы указанные слова и определяя уровень сигнала на выходе схемы логическим пробником, заполните таблицу истинности (табл. 12.13 в разделе "Результаты экспериментов").
Вычислите промежуточные значения и занесите их в таблицу истинности (табл. 12.13 в разделе "Результаты экспериментов"). Они определяют логические сигналы на входе третьего элемента 2И-НЕ в схеме (для контроля результатов вычисления можно к его входам подключить логические пробники).

Результаты экспериментов Эксперимент 1. Исследование логической функции И. а). Задание уровней логических сигналов.

б). Экспериментальное получение таблицы истинности элемента И, Таблица 12.4
Входы
Аналитическое выражение для функции
Эксперимент 2. Исследование логической функции И-НЕ. а). Элемент 2И-НЕ, составленный из 2И а НЕ. Таблица 12.5
Входы
Входы
Входы
Аналитическое выражение для функции

Эксперимент 4. Исследование логической функции ИЛИ-НЕ. а). Элемент ИЛИ-НЕ, составленный из ИЛИ и НЕ. Таблица 12.8
Входы
Входы
Число элементов И-НЕ в микросхеме
Bходы


Таблица 12.12
а

Вопросы
1. Что такое логическая переменная и логический сигнал? Какие значения они могут принимать?
2. Что такое логическая функция?
3. Может ли быть логическим сигналом уровень напряжения? Состояние контакта? Свечение светодиода?
4. Какая логическая функция описывает поведение системы пуска трехфазного двигателя (двигатель может быть запущен, если три датчика подтверждают наличие фазных напряжений)?
5. Датчик температуры состоит из контакта, который замыкается (размыкается) при превышении температуры. При замыкании контакта вырабатывается сигнал логической единицы, при размыкании - логического нуля. Какую схему следует использовать для обнаружения срабатывания хотя бы одного датчика пожарной сигнализации? а) при повышении температуры в датчике происходит замыкание контакта; б) при повышении температуры в датчике происходит размыкание контакта
6. Какой сигнал должен быть подан на неиспользуемые входы элемента 8И-НЕ, если требуется реализовать функцию 5И-НЕ?
7. Какой сигнал должен быть подан на неиспользуемый вход элемента 4ИЛИ-НЕ при реализации функции ЗИЛИ-НЕ?
8. В вашем распоряжении имеются логические элементы 2И-НЕ. Как на их основе сделать схему ЗИ? Достаточно ли 4-х элементов 2И-НЕ для выполнения этой задачи?
9. Как будет вести себя схема И, если на одном из входов вследствие внутренней неисправности будет постоянно присутствовать логическая единица? Логический нуль? Составьте таблицу истинности для неисправной схемы ЗИ. Определите поведение схемы И-НЕ при тех же условиях.
10. Как будет вести себя схема ИЛИ, если на одном из входов вследствие внутренней неисправности будет постоянно присутствовать логическая единица? Логический, нуль? Составьте таблицу истинности для неисправностей схемы ЗИЛИ. Определите поведение схемы ИЛИ-НЕ при тех же условиях.
Синтез и исследование логических схем
Задачи для самостоятельного исследования Задача].
Разработать логические схемы для реализации частично определенных логических функции F 4-х аргументов, заданных таблицами. Каждая комбинация значений аргументов двоичных переменных ABCD отображается числом N, равным: 23D + 22C + 2'В + 2°А. Значения функций при неуказанных комбинациях значений аргументов необходимо доопределить для получения схемы с минимальным числом элементов. Минимизацию логической функции проводить с помощью карт Карно или при помощи логического преобразователя.
Разработку провести на базе следующих типов элементов и схем:
• Элементы 2И, 2ИЛИ, НЕ;
• Элементы 2И-НЕ;
• Элементы 2ИЛИ-НЕ;
• Логические схемы серии 74, содержащие указанные элементы.
Пример: таблица 12.15 соответствует таблице 12.14. Таблица 12.14
N
4
6
7
8
9
11
12
13
14
15
Р
0
1
1
0
1
1
0
0
0
1
Таблица 12.15
N
D
C
B
А
F
4
0
1
0
0
0
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
0
9
1
0
0
1
1
11
1
0
1
1
1
12
1
1
0
0
0
13
1
1
0
1
0
14
1
1
1
0
0
15
1
1
1
1
1
Из карты Карно, составленной при помощи таблицы 12.15, следует, что минимальный вариант решения задачи имеет вид:

Варианты таблиц к задаче 1:
1
N
1
2
3
4
6
7
8
9
11
12
F
0
0
1
0
1
1
0
1
1
0
2
N
0
2
3
5
6
7
8
9
13
15
F
0
1
0
0
1
1
0
0
1
0
3
N
1
2
3
4
6
7
9
12
13
14
F
0
1
1
0
1
0
0
1
0
1
4
N
0
2
3
5
6
7
8
10
12
13
F
0
1
1
0
0
1
1
1
0
0
5
N
0
1
3
4
6
9
10
11
14
15
F
0
1
0
0
0
1
0
1
1
1
6
N
0
1
2
5
7
10
11
13
14
15
F
0
0
0
1
0
1
0
1
1
1
7
N
1
3
4
5
6
10
11
12
14
15
F
0
0
1
0
0
1
1
1
1
0
8
N
0
2
4
5
6
8
10
11
14
15
F
1
0
0
0
0
1
1
1
0
1
9
N
0
1
3
4
5
6
9
10
11
14
F
0
1
0
1
1
0
1
0
1
0
10
N
0
1
2
4
5
7
10
11
13
15
F
1
0
0
1
1
0
0
0
1
1
Задача 9.
Вызовите генератор слов и логический анализатор. Запрограммируйте генератор на формирование последовательности четырехразрядных слов, соответствующих числам натурального ряда от 0 до 15. Подключите его выходы к соответствующим входам схемы, приведенной на рисунке (А - младший разряд числа, D - старший). Исследуйте работу схемы в режимах "STEP" и "CYCLE".

Нарисуйте временные диаграммы сигналов на выходах всех логических элементов схемы для всех возможных комбинаций входных сигналов. Проверьте правильность выполнения задания с помощью логического анализатора. Задача 10.
Проведите анализ работы схемы, изображенной на рисунке, для чего составьте таблицы реализуемых функций, если сигнал в точке 1 воспринимается элементом ИЛИ а) как логическая 1, б) как логический 0. Выберите необходимые инструменты для проведения экспериментальной проверки схемы и определите, как воспринимается сигнал на неподключенном входе при работе базовых элементов.

Задача 11.
Определите, как изменится работа схемы, приведенной в задаче 8, если произошел обрыв во входной цепи одного из элементов И, как показано на рисунке. Изменится ли характер восприятия сигнала на оборванном входе при замене логического элемента И на ИЛИ?

Задача 12.
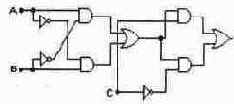
Проведите анализ работы логического устройства, собранного на микросхемах 7404 и 7410, показанного на рисунке. Определите, какую математическую операцию выполняет данное устройство, если комбинации логических уровней на входе рассматривать как числа. Соберите схему, подключите необходимые приборы и проведите экспериментальное исследование работы схемы.

Задача 13.
Составьте логическое выражение, описывающее работу схемы, приведенной на рисунке. Определите, какую математическую операцию выполняет данная схема. Преобразуйте схему таким образом, чтобы получить устройство для выполнения той же операции над двумя 4-разрядными числами.

Задача 14.
Разработайте схему устройства, которое формирует на выходе сигнал, равный 1 при выполнении условия N1>N2, где N1 и N2 - трехразрядные числа, определяемые комбинациями логических уровней на входах схемы. Выполните задание: а) на элементах И, ИЛИ и НЕ; б) на элементах ИСКЛЮЧАЮЩЕЕ ИЛИ, И, НЕ. Укажите, какая элементная база позволяет получить более простые схемотехнические решения устройств сравнения. Задача 15.
Разработайте схему, формирующую на выходе сигнал F из входных сигналов А, В, С, как показано на рисунке.

Соберите схему. При проверке ее работы для формирования входных сигналов используйте: а) источники логических сигналов, б) генератор слов. Задача 16.
Разработайте схему, содержащую минимально возможное число базовых элементов, работа которой описывается временными диаграммами на рисунке (А, В, С - входы, F - выход схемы).

Задача 17.
Произведите изменения в приведенной на рисунке схеме, необходимые для того, чтобы она реализовала ту же функцию, что и в задаче 16. Указание: Минимальные изменения требуют введения элемента НЕ в разрыв одной из цепей.
Задача 18.
Как можно упростить схему предыдущей задачи, чтобы выполняемая схемой функция не изменилась? Задача 19.
При монтаже схемы, приведенной на Рис. а, была допущена ошибка: вместо элемента исключающее ИЛИ был использован элемент ИЛИ (Рис. б). Найдите комбинации входных сигналов, которые позволяют выявить ошибку монтажника.
